 Kosmos
Kosmos
---我们总得选择一条路去前行---
目录
学习笔记|红黑树的故事
学习笔记|红黑树的故事
红黑树是一个平衡二叉树,他的左右子树的高度不能相差超过1
节点结构
颜色(color),左子树指针(left),右子树指针(right),父节点指针(parent),数值(value)
规则
- 每一个节点都是有颜色的,红色或者黑色
- 根的颜色是黑色的
- 叶子节点也是黑色的(指的是不存在的叶子结点)
- 两个红色节点不能相连(两个黑色节点可以)
- 从任意一个节点出发到叶子结点,路过的黑色节点数量相等
旋转
左旋
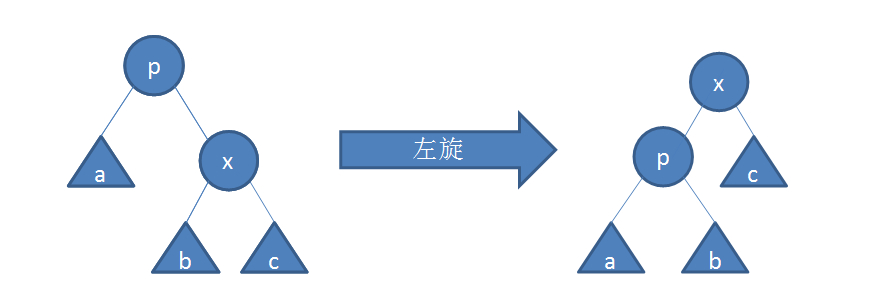
右旋

新节点的插入
插入规则
- 插入的节点默认是红色的
- 假如插入节点的父节点是黑色的,则不会变形
- 假如插入节点的父节点是红色的,要通过重新着色或者是旋转来保持平衡
插入情况
根节点
直接插入并且设置为黑色
父节点是黑色节点
直接插入,颜色为红色
父节点是红色节点,叔叔节点也是红色节点
将父和叔节点设为黑色,爷爷节点(父节点的父节点)设为红色,同时将爷爷节点作为新节点向上检查颜色(递归处理)
父节点是红色节点,叔叔节点是黑色或者不存在,新节点是父节点的右节点
情况一:左旋+变色
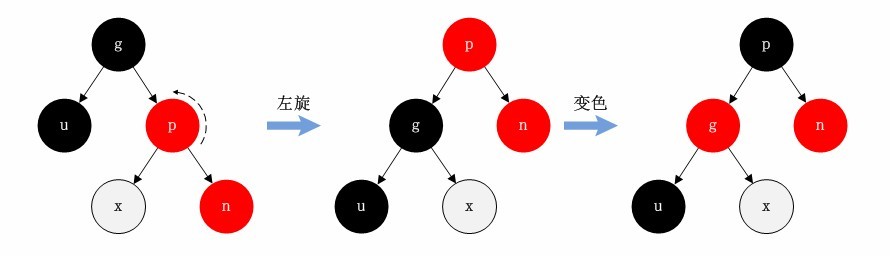
情况二:左旋+右旋+变色
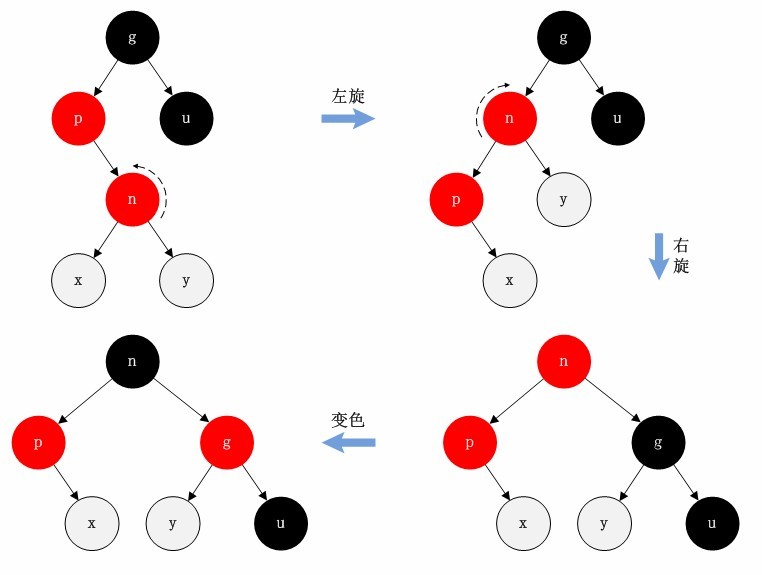
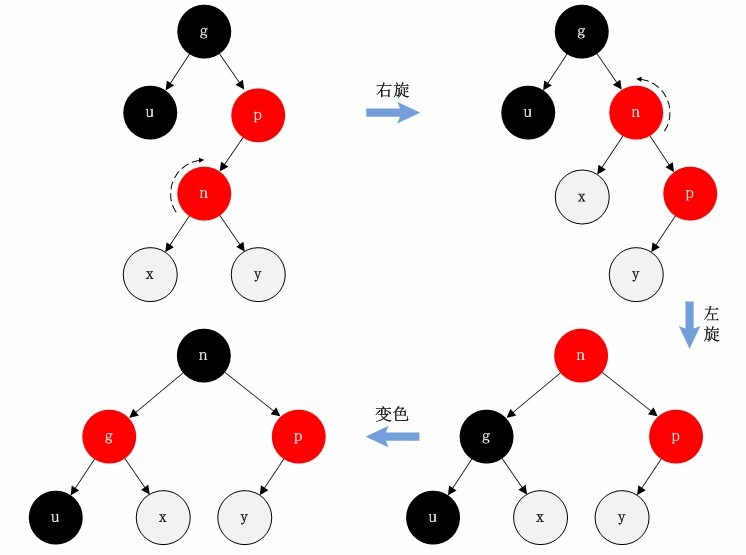
父节点是红色节点,叔叔节点是黑色或者不存在,新节点是父节点的左节点
情况一:右旋+变色
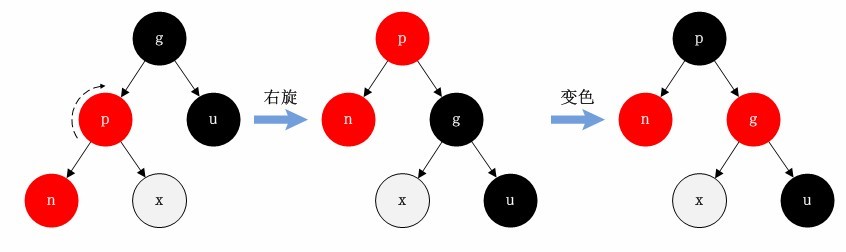
情况二:右旋+左旋+变色
节点的删除
节点的删除并不是真正的删除,而是用其后继节点来代替它(值拷贝),然后删除原来的后继节点就好了
- 假如删除的是红色节点,由于黑色节点的个数不会变,所以红黑树的性质不会改变,假如是黑色节点,要判断是否改变颜色(❤️注意这句话)
- 是叶子节点,直接删除
- 只有一个子节点,用子节点代替删除的节点并删除原来的子节点
- 有两个子节点(子节点是要删除的后继节点的父节点的子节点)
- 删除节点的兄弟节点是红色节点
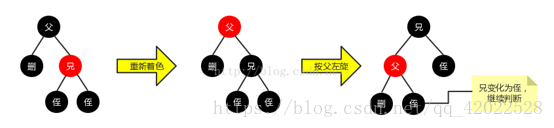
- 删除节点的兄弟节点是黑色节点,且只有右节点
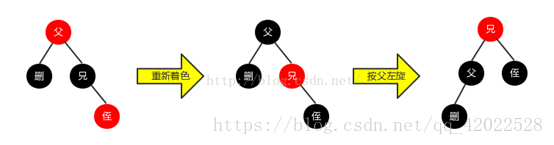
- 删除节点的兄弟节点是黑色节点,且只有左节点,得到的结果是第二种情况
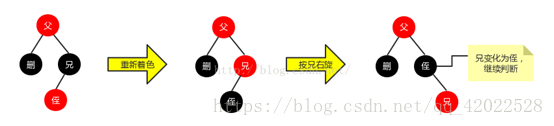
- 删除节点的兄弟节点是黑色节点,且有两个节点(n是删除节点)
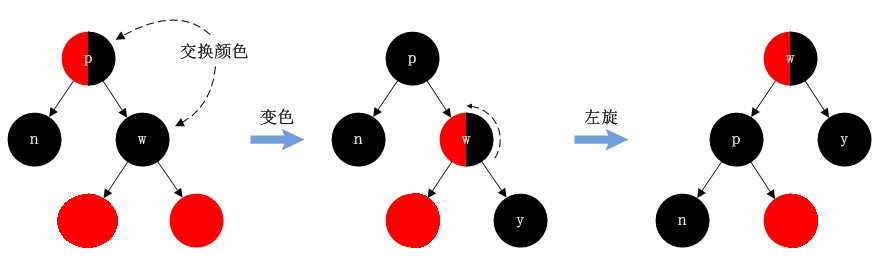
- 删除节点的兄弟节点是红色节点
